Exponentes fraccionarios

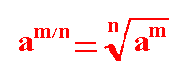
Para transformar una raíz en una potencia:

1º Escribimos el radicando

2º Lo elevamos a la unidad dividida por el índice de la raíz:

Ejemplos:

Ecuaciones con radicales

La ecuaciones con radicales son aquellas que contienen la variable desconocida bajo un radical.

Resolución de ecuaciones con radicales:

1) Aislar el radical a un sólo lado de la ecuación
2) Elevar al cuadrado ambos lados de la ecuación para eliminar el radical
*Depende del índice del radical (si el índice es tres, se eleva a la tres, etc.)

3) Resolver la ecuación obtenida
4) Verificación con las soluciones obtenidas
5) Si la ecuación tiene varios radicales, se repiten los dos primeros pasos del proceso hasta eliminarlos todos

Fracciones Complejas

Ejemplos:

__________________________________________________________________________

En este vídeo se presenta una forma poco común de simplificar fracciones complejas.

Ecuaciones racionales

Para resolver ecuaciones racionales se multiplican ambos miembros de la ecuación por el mínimo común múltiplo de los denominadores.

1) Factorice los denominadores
2) Hallar el MCD
3) Multiplicar por el MCD toda la ecuación
4) Propiedad distributiva para cada término de la ecuación
5) Cancelar los denominadores
6) Ahora tienes una ecuación normal, sin denominadores, despejar para la variable desconocida

- Recuerda comprobar las soluciones (verificar)
- Recuerda igualar a CERO cuando tengas términos cuadráticos

Ejemplo:

Suma y Resta de Expresiones Racionales

Cuando las fracciones son heterogéneas

Proceso:
1) hallar el mínimo común denominador (MCD)
2) se dividirá cada expresión racional por el mínimo común denominador y el resultado
se multiplicará por el numerador correspondiente.
3) se suma o resta (según sea el caso) los numeradores y se escribe todo sobre un mismo
denominador
4) se simplifica la expresión racional resultante.

Ejemplo con operaciones combinadas:

Expresiones Racionales: Simplificación

Procedimiento para simplificar expresiones racionales:

1) Factorice completamente el numerador y denominador
2) Cancele aquellos factores que sean comunes (iguales) en el
numerador y en el denominador

Factorización: Trinomios de la forma x^2+bx+c

RECUERDA: Hallar dos factores de c tal que la suma de esos factores sea igual a bx

Ejemplo: x² + 6x + 8 = (x + 4)(x + 2)

Ejemplo: x² + 9x - 52 = (x +13)(x - 4)

Ejemplo: x² - 2x - 15 = (x - 5)(x + 3)

Factorización: Suma y diferencia de cubos

Suma de cubos perfectos
Procedimiento:
1) extraer la raíz cúbica de a y b

2) se forma un producto de dos factores

3) los términos del binomio van a ser la suma de las raíces cúbicas a y b

4) los términos del trinomio quedan de la siguiente forma:
a) el cuadrado de la primera raíz
b) MENOS el producto de a y b
c) MÁS el cuadrado de la segunda raíz

Ejemplo: Factorizar 125x³ + 1000
La raíz cúbica de: 125x³ es 5x
La raíz cúbica de: 1000 es 10

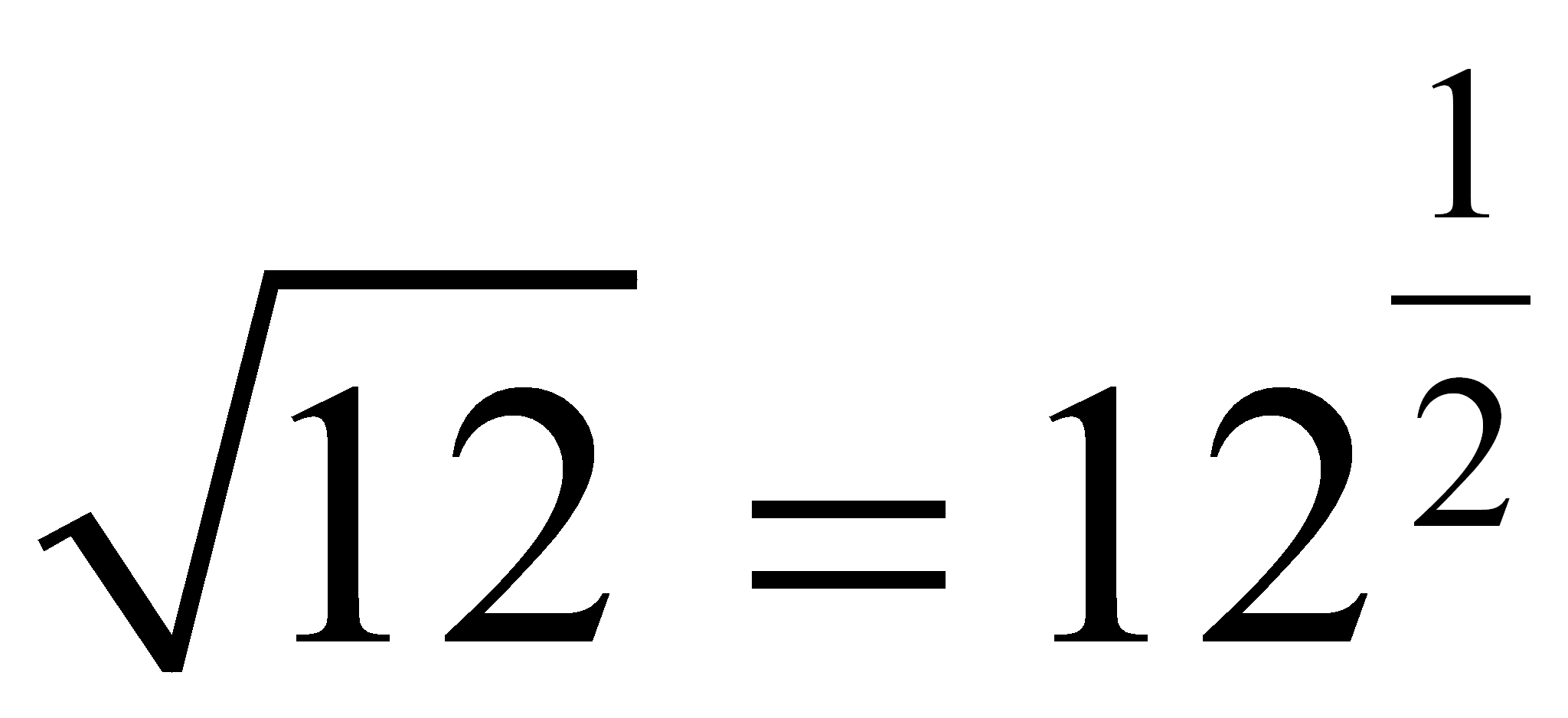
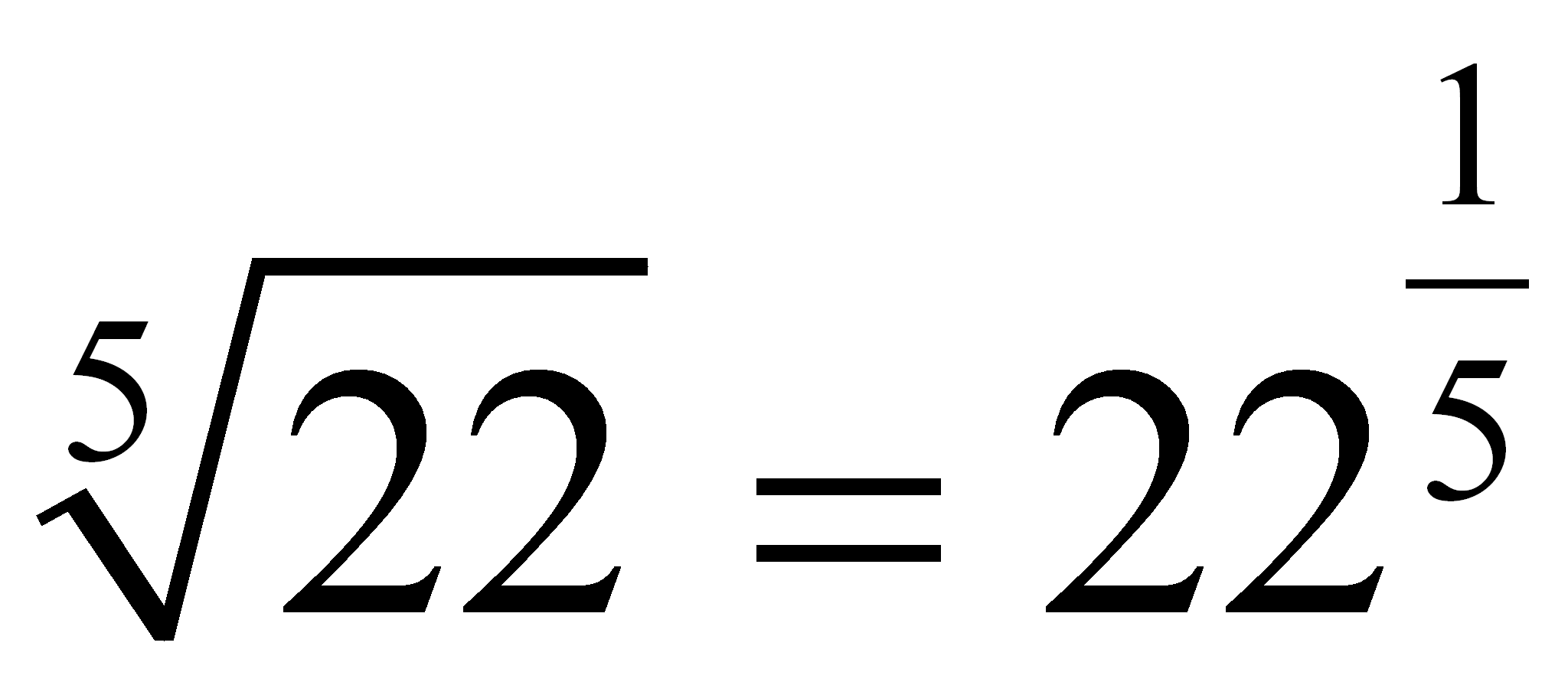
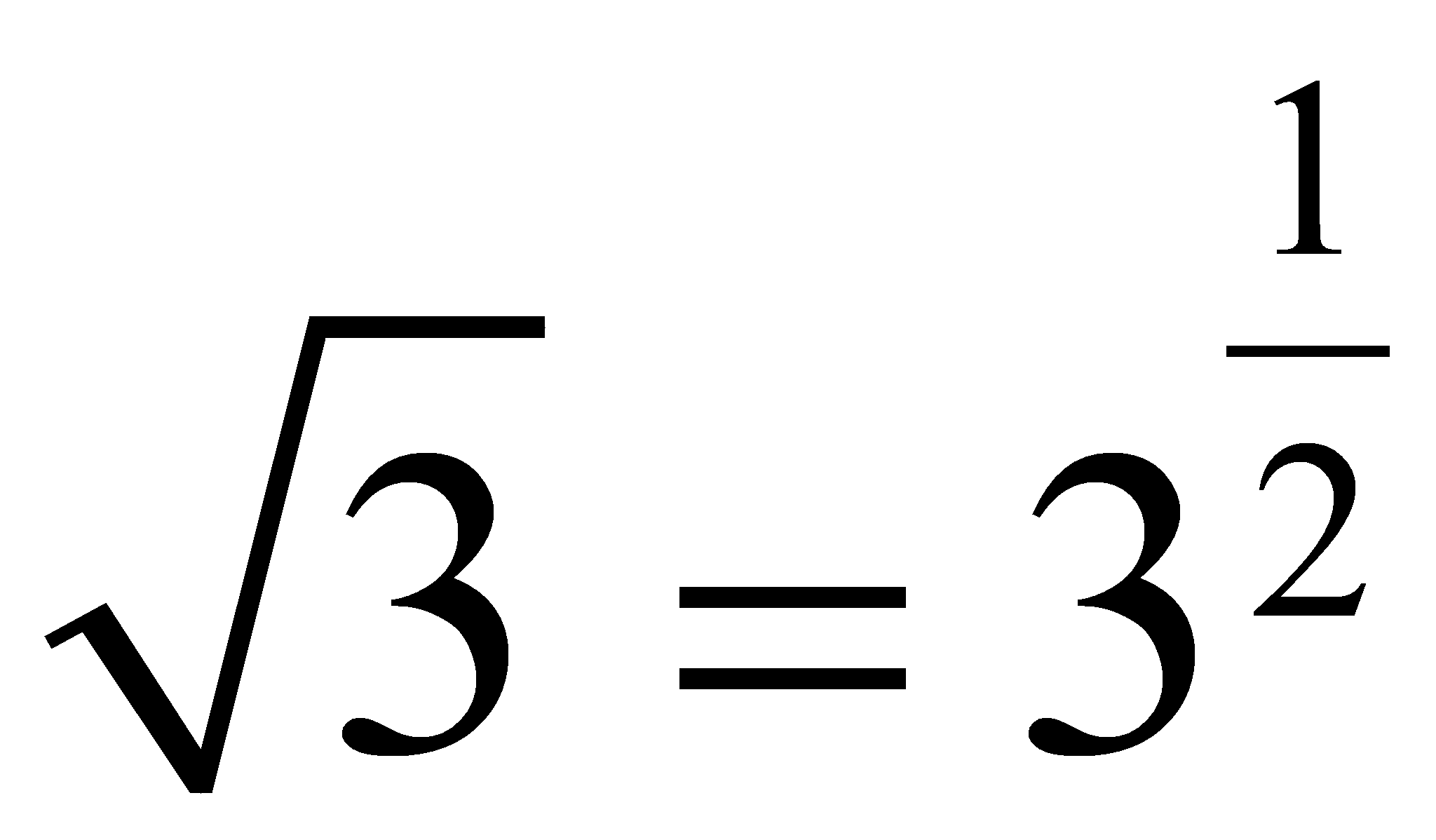
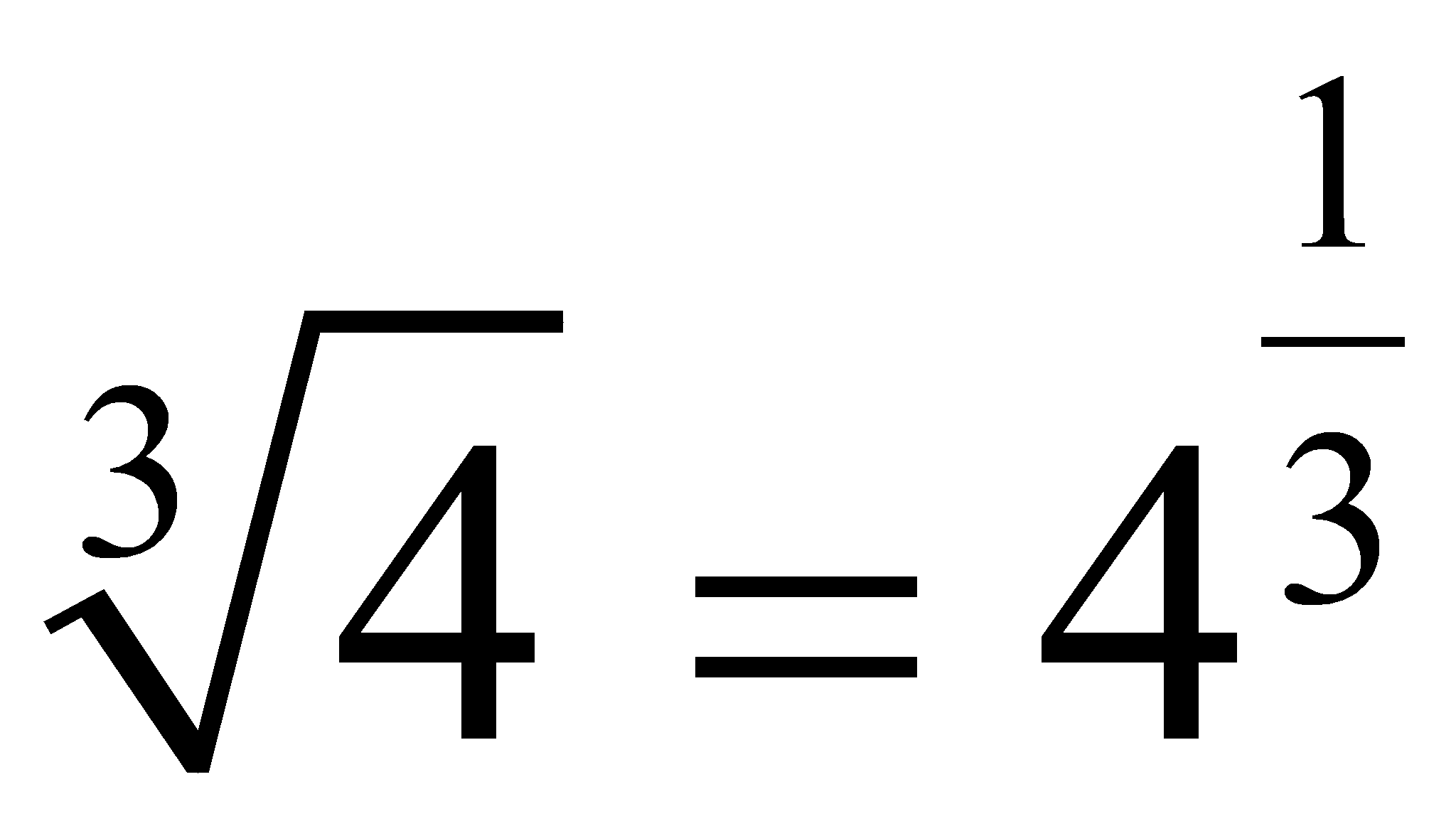
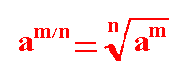
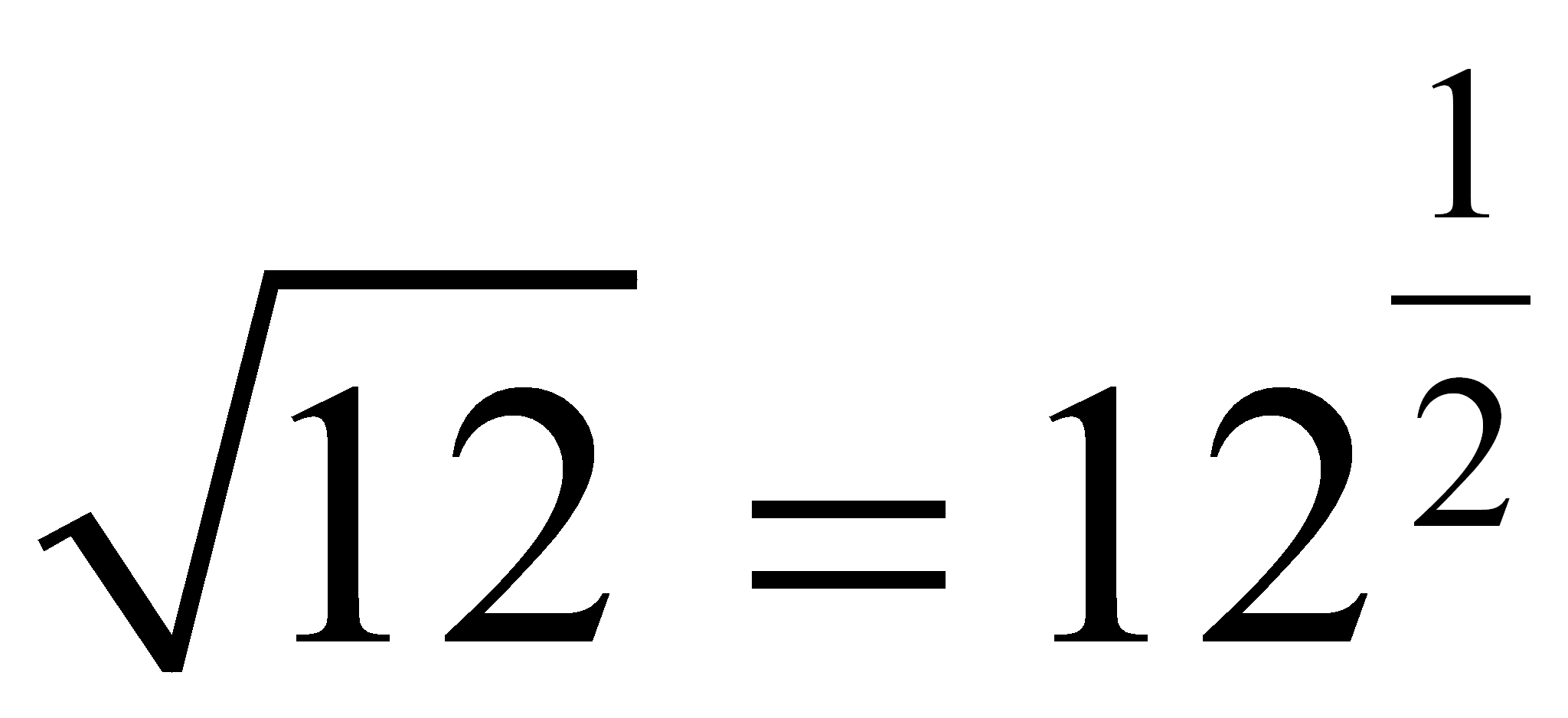
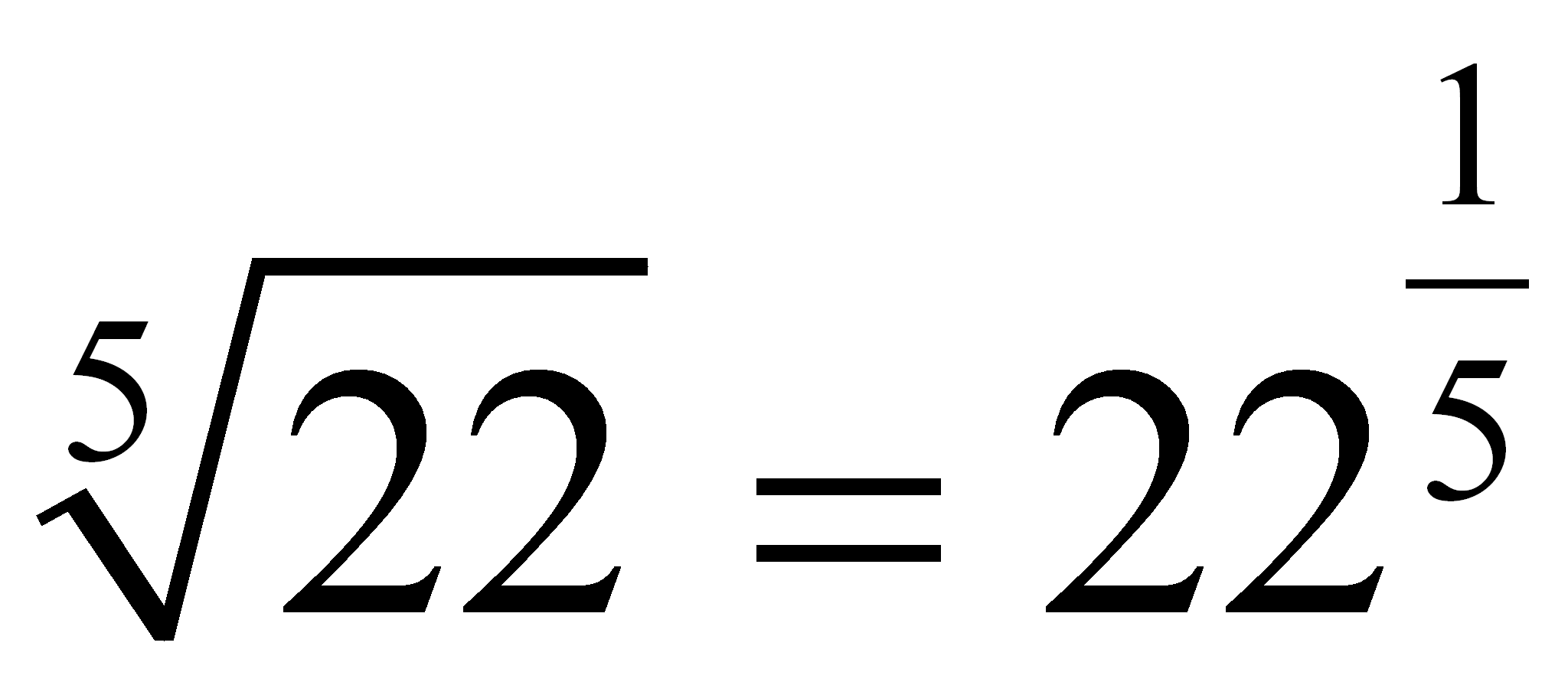
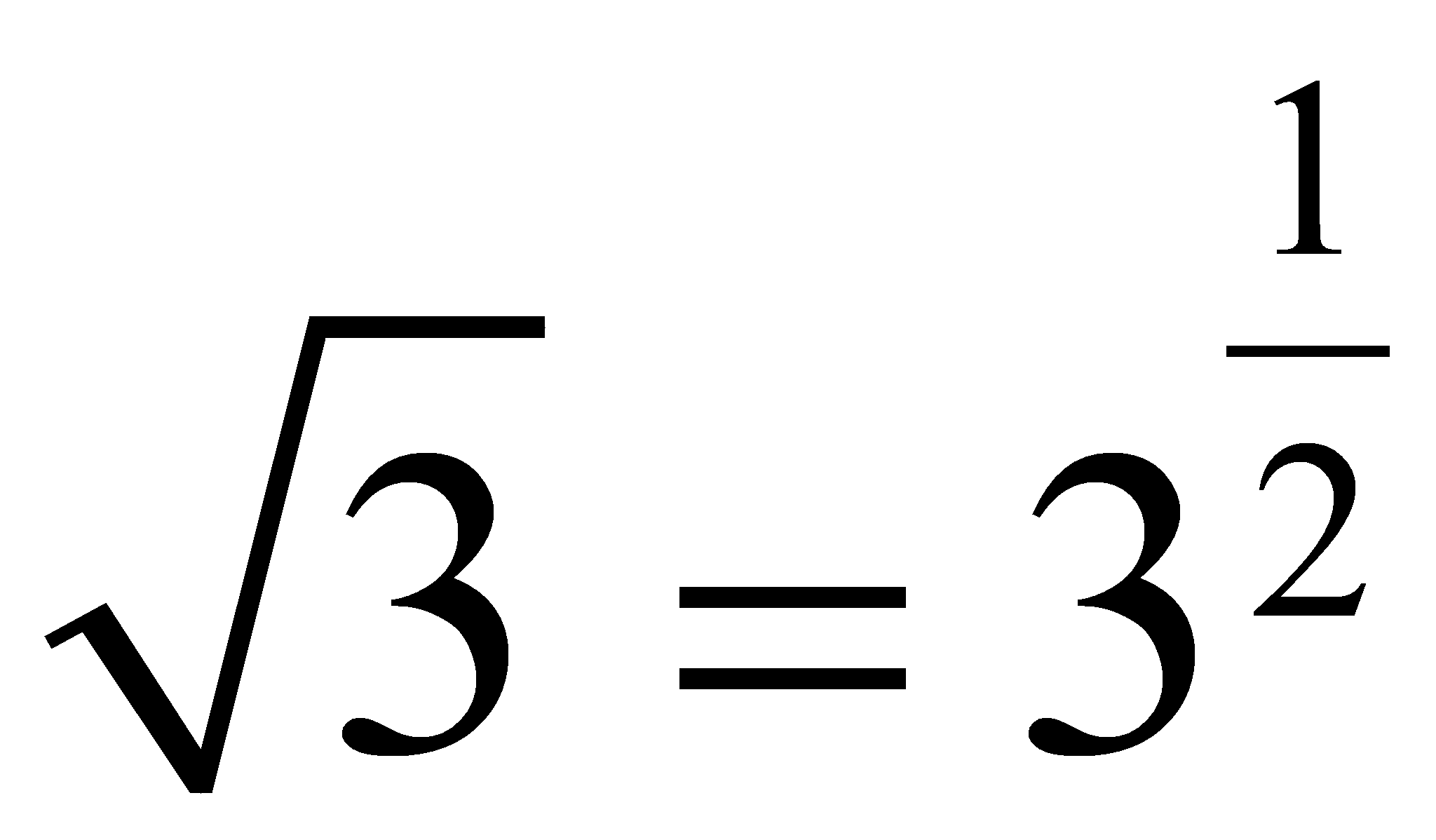
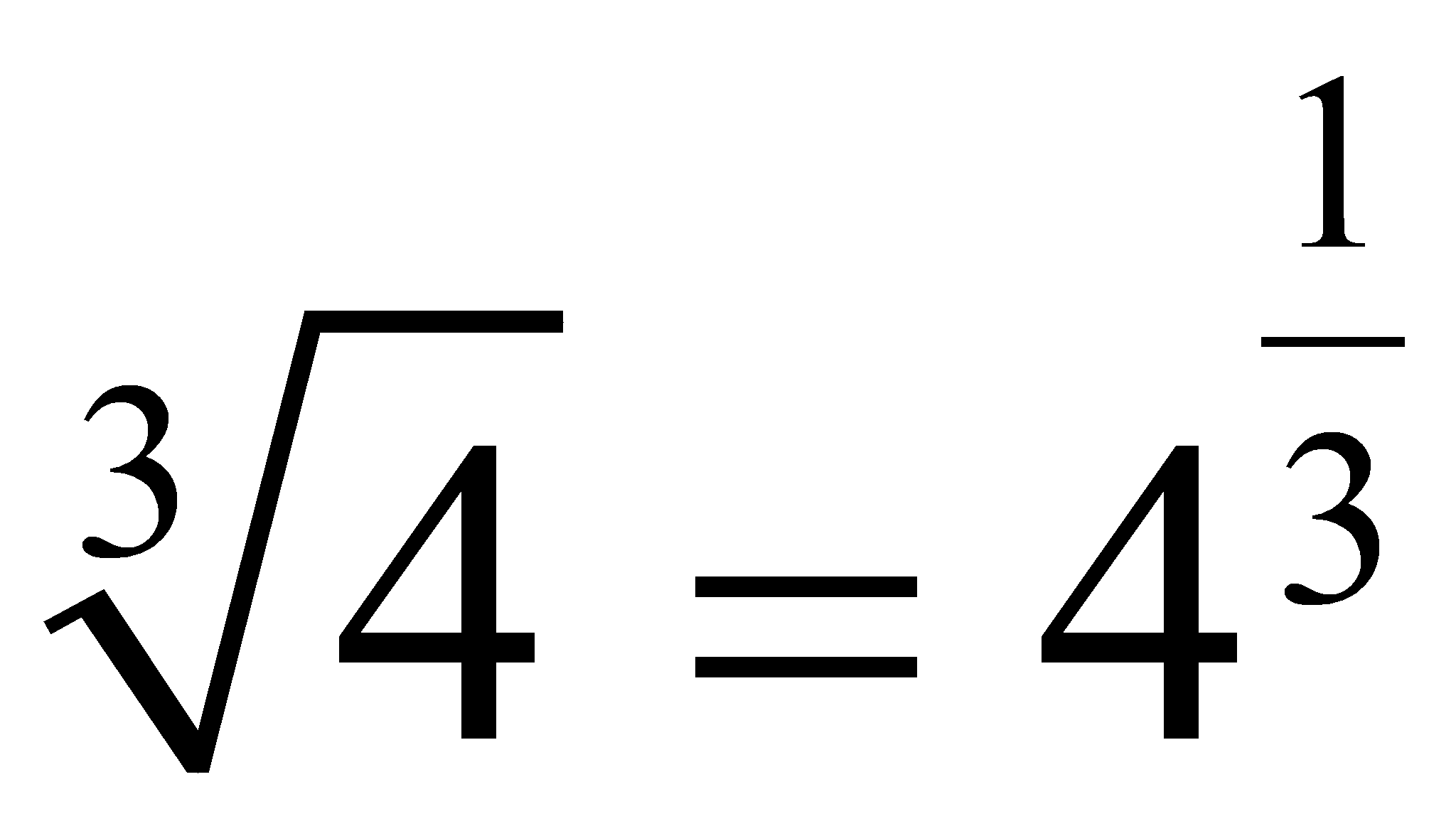
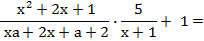
Según procedimiento:

125x³ + 1000

(5x + 10)[(5x)² - (5x)(10) + (10)²]

Por lo tanto: 125x³ + 1000

(5x + 10) (25x² - 50x + 100)

Factorización: Trinomios cuadrados perfectos

Regla para reconocer un trinomio cuadrado perfecto:

1) si el primer y tercer término son cuadrados perfectos

2) si el segundo término es el doble del producto de sus raíces cuadradas (2ab)

Factorización: Factor Común (Caso especial)

Cuando el factor común que aparece es un polinomio.

c(a + b) + d(a + b) + e(a + b)=(a + b)( c + d + e )

Procedimiento para factorizar:

	1) Se extrae el factor común de cualquier clase, que viene a ser el primer factor.
	2) Se divide cada parte de la expresión entre el factor común y el conjunto viene a ser el segundo factor.